Wenn man software defined radios bauen will, ist es nützlich, neben digitalen Filtern, digitalen Mischern, digitalen Modulatoren und Demodulatoren auch digitale Signalquellen zu haben, ähnlich wie in der Analogtechnik.
Die gibt es natürlich, und diese digitalen Signalquellen nennt man NCOs, numerically controlled oscillators.
Das Verfahren, das zum Erzeugen von digitalen Kurvenformen verwendet wird, nennt sich DDS, direct digital synthesis.
Wie funktioniert DDS?
Zunächst schauen wir uns mal ein ganz einfaches Verfahren zum Erzeugen eines Sinussignals mit digitalen Mitteln an.
Dieses Verfahren hat vielleicht schon der eine oder andere von Euch in der Vergangenheit selber schon mal ausprobiert.
Ein ganz einfacher digitaler Sinusgenerator
Ich kann mich erinnern, als Schüler, Anfang der Achtzigerjahre, etwa 1981, ziemlich genau sowas gebaut zu haben:
Zu meinem damaligen Einplatinencomputer SYM-1 hatte ich mir auf eine Lochrasterplatine einen Textool-Sockel gebaut, darauf war noch ein Spannungswandler von 5V auf 25V, den ich bei Radio-RIM zufällig preiswert bekommen habe, und dazu habe ich mir ein kleines Assemblerprogramm geschrieben, und schon konnte ich ein EPROM vom Typ 2716 programmieren.
Das EPROM 2716 war toll, weil es nur 5V Betriebsspannung brauchte, 2 kbyte Daten fasste und per UV-Desinfektionslampe innerhalb einer halben Stunde oder so wieder gelöscht werden konnte.
(Das EPROM 2708 hätte zwar für dieses Experiment auch gereicht, brauchte aber außer +5V noch -5V und +12V UND die 25V Programmierspannung)
An die Adressleitungen des EPROMs hatte ich einen 8-bit-Zähler angeschlossen (wahrscheinlich zwei 74LS193, aber das weiß ich heute nicht mehr so genau).
Die Datenausgänge des EPROMS gingen an einen 8-bit-DAC, ich glaube das Ding hieß DAC08, den es heute noch ![]() gibt.
gibt.
Mit dem Basic-Interpreter meines SYM-1 konnte ich mir eine 256 Einträge lange Sinustabelle berechnen, die ich anschließend ins EPROM programmierte.
Den 8-bit-Zähler konnte man mit einer Taktfrequenz von bis zu ca. 1 MHz betreiben, das war ungefähr die Frequenz, für die das EPROM und der DAC ausgelegt waren.
Weder das EPROM noch der DAC08 waren synchrone Bauteile, d.h. sie hatten keinen Takteingang, arbeiteten also asynchron, was bei einem EPROM bedeutet, dass sich die Daten ändern, kurz nachdem sich die Adressen geändert hatten, eben ungefähr nach der Zugriffszeit.
Der DAC verhielt sich genauso asynchron.
Es wäre also aus heutiger Sicht – damals war mir das noch gar nicht richtig klar – zu erwarten gewesen, dass die Kurvenform, die aus dem DAC herauskam, von Glitches und Spikes an den Übergangsstellen der DAC-Werte übersät gewesen war.
An so was kann ich mich nicht mehr erinnern, aber das liegt möglicherweise daran, dass das 1-Kanal-Tektronix-Röhrenoszilloskop, das ich damals von einem Nachbarn geschenkt bekommen hatte, eine viel zu kleine Bandbreite hatte, um diese Spikes anzuzeigen.
Und außerdem war ich vermutlich viel zu happy, dass die ganze Geschichte überhaupt funktionierte, als dass mir solche „Kleinigkeiten“ überhaupt aufgefallen wären.
Welche Frequenz kam also aus dem DAC raus?
Na ja, ganz einfach die Taktfrequenz dividiert durch die Anzahl der Samples der Sinusschwingung, die im EPROM gespeichert waren, also
1 MHz / 256 = 3906,25 Hz.
Diese Frequenz konnte ich damals durch Frequenzteilung weiter verkleinern (193,124 Hz; 976,5625 Hz usw.), aber das war’s dann auch schon.
Viel kann man mit so einem Sinusgenerator nicht anfangen!
Wenn es damals schon das Internet gegeben hätte oder wenn ich Zugriff auf Fachliteratur über eine Bibliothek gehabt hätte und wenn mir jemand natürlich einen entsprechenden Tipp gegeben hätte dann hätte ich ein damals auch schon 10 Jahre altes Paper lesen können, worin das DDS-Verfahren schon beschrieben war:
J. Tierney, C. Rader, and B. Gold „A Digital Frequency Synthesizer,“ IEEE Trans. Audio and Electroacoust., Vol. AU-19, pp. 48-57, Mar. 1971.
Mit ein paar mehr TTL-Bauteilen (ok, es wäre schon ein ziemlich großer Aufbau geworden, und TTL-ICs waren auch nicht ganz billig damals) hätte ich nämlich etwas weitaus besseres anstellen können: Ich hätte im Prinzip auch damals schon einen quarzgenauen Frequenzgenerator nach dem DDS-Verfahren mit bis zu ein paar hundert kHz Grenzfrequenz mit ultra-hoher Frequenzauflösung bauen können, den ich mit meinem Mikrocontroller steuern hätte können und der alle analogen Funktionsgeneratoren der damaligen Zeit um Längen geschlagen hätte!
DDS war also schon 1971 erfunden worden, die Schaltungstechnik wäre auch umsetzbar gewesen, wenn auch etwas aufwändig, aber es dauerte noch etwa 25 Jahre, bis diese Technik als Komplettlösung in einer einzigen integrierten Schaltung zu günstigen Preisen zur Verfügung stand.
Aber schauen wir uns zunächst einmal den simplen Sinusgenerator an:
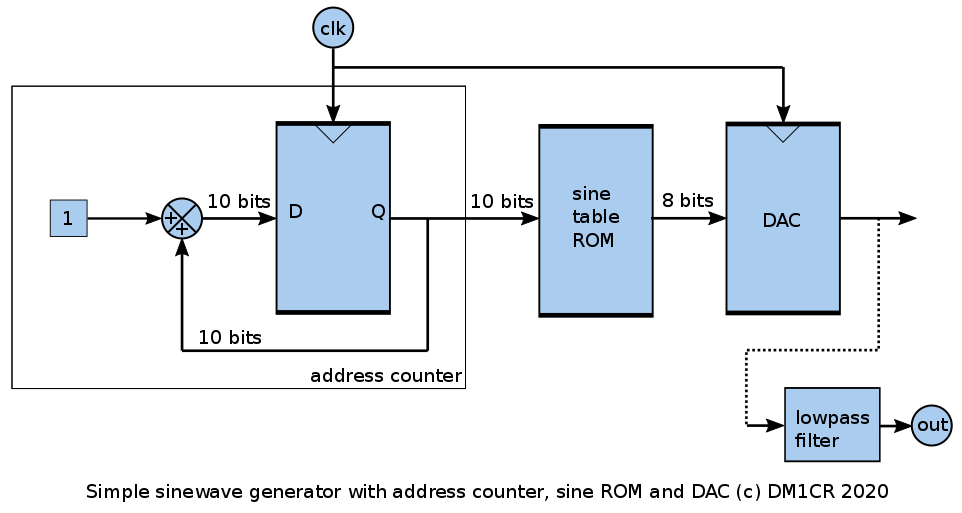
Dieses Blockschaltbild zeigt sogar schon eine verbesserte Version mit synchronem DAC und einem 10-bit-Wort als Eingangsdatum für die Sinustabelle.
An der Ausgangsfrequenz ist nichts zu ändern, solange man nicht die Taktfrequenz des Zählers ändert.
Der Adresszähler, der die Adressen des EPROMS hochzählt, ist als Addierer mit Register dargestellt.
Die Gründe dafür werden gleich deutlicher.
Bei jeder Flanke des Taktsignals wird zu dem aktuellen Stand des Registers die Zahl „1“ dazugezählt, d.h. am Ausgang des Registers erhält man die Zahlen bzw. Adressen 0, 1, 2, 3, …, 254, 255, 0, 1, 2, …
Wenn der Addierer überläuft dann beginnt alles wieder von vorn.
Und jetzt kommt DDS!
Die folgende Grafik zeigt das Blockschaltbild eines DDS-Generators.
Der Aufbau ist dem simplen Aufbau von vorher nicht unähnlich:
Es gibt einen DAC, der aus dem Digitalwert an seinem Eingang ein analoges Ausgangssignal macht, d.h. einen Strom oder eine Spannung ausgibt.
Es gibt eine Sinustabelle in einem ROM oder einer anderen Art von adressierbarem Speicher, der passend zum Eingangswort am Eingang einen digitalen Sinuswert am Ausgang ausgibt.
Das ist alles so wie vorhin; das könnten sogar die identischen Bauteile sein, es würde alles prima funktionieren!
Es gibt auch ein Phasenregister und einen Addierer, der das Eingangswort für die Sinustabelle liefert.
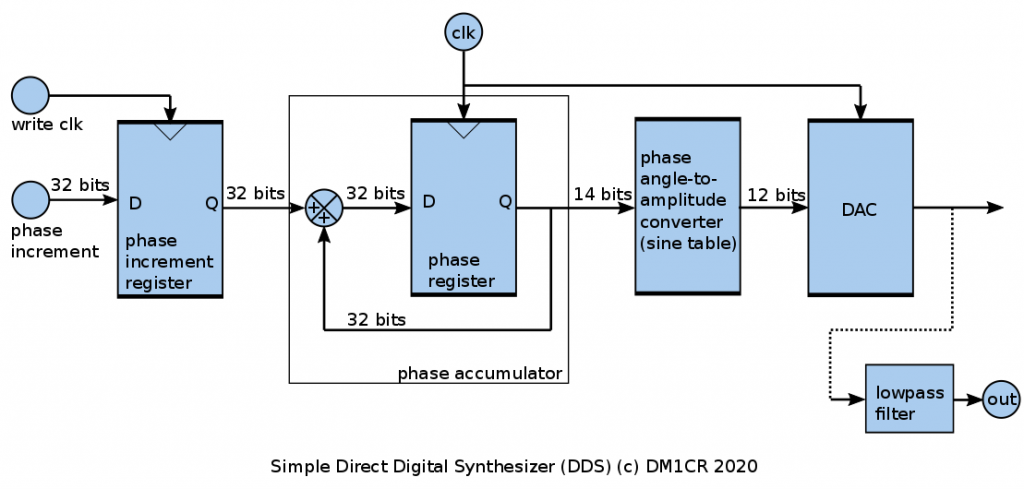
Hier gibt es aber einen wesentlichen Unterschied:
Während der Adresszähler des ersten Sinusgenerators bei jedem Takt um „1“ hochzählt und nur 8 bit breit ist, besteht dieser Adresszähler aus einem viel breiteren Register, Phasenregister genannt, von typ. 32-48 bit Breite.
Dieser Zähler zählt auch nicht fest eingestellt um „1“ hoch, sondern kann mit einer Schrittweite hochzählen, die in ein Register geladen werden kann, das Phaseninkrementregister, und das ebenfalls 32-48 bit Breite besitzt so wie das Phasenregister. Der Addierer zusammen mit dem Phasenregister wird übrigens oft Phasenakkumulator genannt.
Es gibt (noch) keine DACs mit 32..48 bit Auflösung, und man braucht sie für das DDS-Prinzip auch nicht unbedingt.
Schnelle DACs mit guten dynamischen Eigenschaften (welche das sind und was „schnell“ heißt, kommt später) gibt es von ca. 8 bit bis 16 bit, im Audio-Bereich bis ca. 24 bit.
Gehen wir für unser Beispiel von einem 32 bit breiten Phasenregister und einem 12-bit-DAC aus.
Man braucht außerdem eine Sinustabelle, die Werte für unseren 12bit-DAC ausgeben kann.
Wenn man nur wenig Verlust durch Rundungsfehler machen will, dann sollte man die Eingangsworte der Sinustabelle etwas breiter als 12 bit machen, sagen wir 14 bit (weil die Sinusfunktion hat nur im Nulldurchgang die Steigung 1, aber zu den Minima und Maxima hin wird die Steigung immer flacher und bei festgelegter DAC-Bitbreite wird die Signalqualität besser, wenn zumindest das Argument des Sinus mit höherer Genauigkeit angeliefert wird!)
Die 14 bits für die Eingangsworte der Sinustabelle werden an die obersten bits (die 14 MSBs) des Phasenregisters angeschlossen.
Die unteren Bits werden nicht an die Sinustabelle angeschlossen.
Alle 32 Bits des Phasenregisters werden zum Addierer-Eingang zurückgeführt, zum Phaseninkrement-Wert dazuaddiert und erscheinen einen Takt später am Ausgang des Phasenregisters.
Die Bits 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17 stellen also gewissermaßen die Nachkommastellen der Zahl dar, deren Vorkommastellen, die Bits 18,19,20,21,22,23,24,25,26,27,28,29,30,31 abgeschnitten und für das Eingangswort der Sinustabelle verwendet werden.
Übertragen auf unseren simplen Frequenzgenerator, hat man bei einem DDS die Möglichkeit, nicht nur „1“ bei jedem Takt zum Eingangswort dazu zu addieren, sondern auch größere Zahlen als „1“ und Zahlen mit Nachkommastellen!
Wenn man nur Bit 0 auf 1 setzt, dann erhält man die kleinste Frequenz, die der Generator ausgeben kann.
Gleichzeitig ist das auch die Frequenzauflösung.
Erst wenn das Phasenregister überläuft und auf 0 zurückspringt, wurde eine Periode der Sinusschwingung ausgegeben.
Die Frequenzauflösung errechnet sich deswegen aus dem Quotienten der Taktfrequenz und dem Modulus des Zählers.
Frequenzauflösung = fclock/2**N
mit N = Bitbreite des Phasenregisters
Beispiel: Taktfrequenz = 1 MHz, N = 32
-> delta_f = 1 MHz/2**32 = 232,83 µHz
Die Maximalfrequenz entspricht der Nyquist-Frequenz, also der halben Taktrate, in diesem Fall also 500 kHz (in der Praxis deutlich weniger, aber das hängt von der Selektivität des Tiefpassfilters ab).
In diesem Fall, also bei der Nyquist-Frequenz, wird aber nichts Sinus-ähnliches mehr ausgegeben, sondern nur noch 2 Spannungswerte mit abwechselnd positivem und negativem Vorzeichen. Das macht aber nichts, denn ein richtig dimensioniertes Tiefpassfilter macht da wieder einen schönen Sinus draus.
Moderne DDS-Bausteine lassen sich übrigens heute zum Teil bis in den GHz-Bereich hinein takten.
Für diese Taktung im GHz-Bereich muss außen trotzdem nur ein Quarz im 10…50-MHz-Bereich angeschlossen werden; die interne Frequenzvervielfachung mittels PLL ist bei diesen Bausteinen auch schon eingebaut.
Damit ist eine hochstabile Signalerzeugung mittels DDS bis in den Mehrere-Hundert-MHz-Bereich kein Problem mehr!
Lesenswerte Lektüre:
https://www.analog.com/media/cn/training-seminars/tutorials/450968421DDS_Tutorial_rev12-2-99.pdf
Kommentare?

Hmmmm