Wozu braucht man einen Bandpassfilter für 6070 kHz?
Wer es noch nicht wissen sollte: Jeden Sonntag von 11h bis 12h sendet der Deutsche Amateur-Radio-Club https://www.darc.de/nachrichten/radio-darc/ über den Sender Moosbrunn https://de.wikipedia.org/wiki/Sender_Moosbrunn auf Kurzwelle bei 6070 kHz (49 m) mit AM-Modulation ein einstündiges Programm aus.
Wer dieses Programm empfangen möchte, braucht entweder ein altes Kurzwellenradio oder was neueres, selbstgebasteltes, z.B. einen SDR-Empfänger.
Wenn man mit SDR herumexperimentieren möchte, zum Beispiel mit Bandpass-Sampling (https://www.dsprelated.com/showarticle/523.php), dann braucht man unbedingt einen einigermaßen guten Bandpassfilter für diese Frequenz.
Wie man Bandpassfilter als Zweikreis- und Dreikreis-Filter baut (double-tuned filters, triple-tuned filters), beschreiben W7ZOI, KK7B und W7PUA in ihrem wunderbaren Buch „Experimental Methods in RF Design“ in Kapitel 3.
Aus den Berechnungsformeln habe ich ein kleines Python-Skript abgeleitet. Man geht von irgendeinem Wert für die Induktivitäten aus, wobei ein guter Startwert L = 10/f ist, wobei L in Henry und f in Hz gemeint ist. Man sollte auch wissen, dass man mit Eisenpulver-Ringkernen wie T50-6 und T68-2 und Windungszahlen zwischen 5 und 35 mit Leerlaufgüten zwischen 150 und 250 rechnen kann, wie in Tabelle 3A im Buch angegeben.
Hier ist das Skript:
# -*- coding: utf-8 -*-
"""
Created on Tue Apr 27 2021
Version of May 13, 2021
Calculator for Double-Tuned and Triple-Tuned Circuits
@author: DM1CR, using design equations of W7ZOI, KK7B, W7PUA in EMRFD
"""
import math
kq_dtc = { "Butterworth" : [0.7071, 1.414], "0.1dB": [0.7107, 1.638], \
"0.25dB": [0.7154, 1.779], "0.5dB": [0.7225, 1.9497], \
"0.75dB": [0.7290, 2.091], "1.0dB": [0.7351, 2.3167], \
"1.5dB": [0.7466, 2.452] }
kq_ttc = { "Butterworth" : [0.7071, 1.0], "0.1dB": [0.6617, 1.4328], \
"0.25dB": [0.6530, 1.6330], "0.5dB": [0.6474, 1.8640], \
"0.5dB": [0.6474, 1.8640], "0.75dB": [0.6450, 2.0498], \
"0.75dB": [0.6450, 2.0498], "1.0dB": [0.6439, 2.2156], \
"1.5dB": [0.6437, 2.5169] }
def kq(rippleString, poles=2):
if poles == 2:
kqlist = kq_dtc[rippleString]
elif poles == 3:
kqlist = kq_ttc[rippleString]
else:
kqlist = [0,0]
return kqlist
def dttc(F, BW, L=0, Qu=200, R0 = 50, type = "Butterworth", poles=2):
k, q = kq(type, poles)
if L==0:
L = 10/F # default value for inductance if none is given
w = 2.0 * math.pi * F
c0 = 1 / (w*w*L)
c12 = c0 * k * BW / F
qe = q * F * Qu / (BW * Qu - q * F)
ce = 1/w * 1 / math.sqrt(R0 * qe * w * L - R0*R0)
ct = c0 - ce - c12
if poles == 3:
cm = c0 - 2.0 * c12
else:
cm = 0
return{ "F[MHz]": F/1e6, "BW[MHz]": BW/1e6, "L[uH]": L/1e-6, \
"Qu": Qu, "C-end[pF]":ce/1e-12, "C-12[pF]": c12/1e-12, \
"C-tune[pF]": ct/1e-12, "C-M[pF]": cm/1e-12, "R0": R0, \
"type":type}
DTC_49m_0 = dttc(6.07e6, 0.1e6, L=1.156e-6, Qu=250)
print(DTC_49m_0)
TTC_49m_1 = dttc(6.07e6, 0.1e6, L=1.156e-6, Qu=250, poles=3)
print(TTC_49m_1)
Die Funktion dttc steht für „double- or triple-tuned circuit“ und nimmt die Argumente
F: Mittenfrequenz in Hz
BW: Bandbreite in Hz
L: Induktivität der Spulen in H (Beispiel: 17 Wdg. auf einem T50-6-Ringkern ergeben 1.156e µH)
Qu: Leerlaufgüte (Beispiel: mit 17 Wdg. auf einem T50-6-Ringkern erreicht man etwa Qu=250)
R0: Impedanz der angeschlossenen Quelle und der Senke in Ohm
type: „Butterworth“ oder Chebyshev mit „x.xdB“, siehe Code
poles: 2 (default) oder 3
Die Funktion gibt ein Dictionary mit Bauteile-Werten zurück.
Lässt man also obiges Programm laufen, dann erhält man:
{'F[MHz]': 6.07, 'BW[MHz]': 0.1, 'L[uH]': 1.1560000000000001, 'Qu': 250, 'C-end[pF]': 49.060697313841416, 'C-12[pF]': 6.92782953903852, 'C-tune[pF]': 538.7212073001934, 'C-M[pF]': 0.0, 'R0': 50, 'type': 'Butterworth'}
{'F[MHz]': 6.07, 'BW[MHz]': 0.1, 'L[uH]': 1.1560000000000001, 'Qu': 250, 'C-end[pF]': 62.81858158120885, 'C-12[pF]': 6.92782953903852, 'C-tune[pF]': 524.963323032826, 'C-M[pF]': 580.8540750749964, 'R0': 50, 'type': 'Butterworth'}
Man kann jetzt mit den berechneten Daten und LTSpice solche Filter zeichnen und simulieren:
Zum Vergleich habe ich beide Filtertypen simuliert; oben ist das Zweikreisfilter zu sehen (DTC) und unten das Dreikreisfilter (TTC).
Für richtige Simulationsergebnisse muss man eine ideale Spannungsquelle vorsehen und für jedes Filter eine Quellimpedanz von 50 Ohm (oder welche Quellimpedanz man auch immer verwenden will) vorsehen. Wenn man nur einen Filter simulieren will, kann man natürlich der Spannungsquelle selber schon einen Serienwiderstand geben, was eine transiente Simulation etwas beschleunigt.
Auf dem Schaltplan ist nicht zu sehen, dass ich den Induktivitäten eine Leerlauf-Güte gegeben habe. Eine simple Methode dafür ist, einen entsprechenden Parallel- oder Serienwiderstand bei den Eigenschaften von L1…L5 einzustellen.
Ich habe mich für einen Serienwiderstand entschieden.

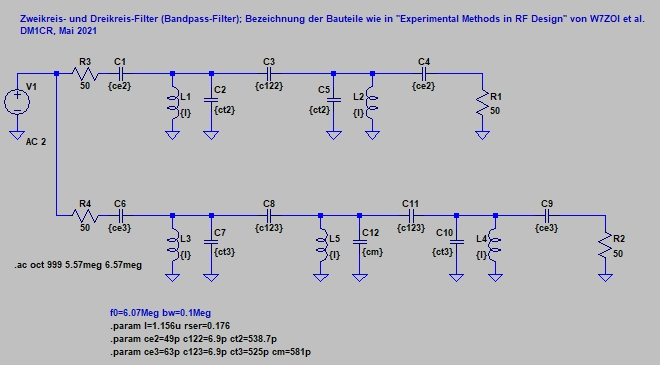
Die Leerlauf-Güte von L1…L5 habe ich als Qu=250 angenommen; daraus resultiert ein Serienwiderstand von
R_ser = 2 * Pi * f * L / Q = 0.176 Ohm, der in der ersten Parameterzeile zu finden ist (rser)
Die LTSpice-Simulationsdatei kann über den folgenden Link heruntergeladen werden:
Die Beträge der Übertragungsfunktionen des Zweikreis- und des Dreikreis-Filters schauen dann in der Simulation wie folgt aus.
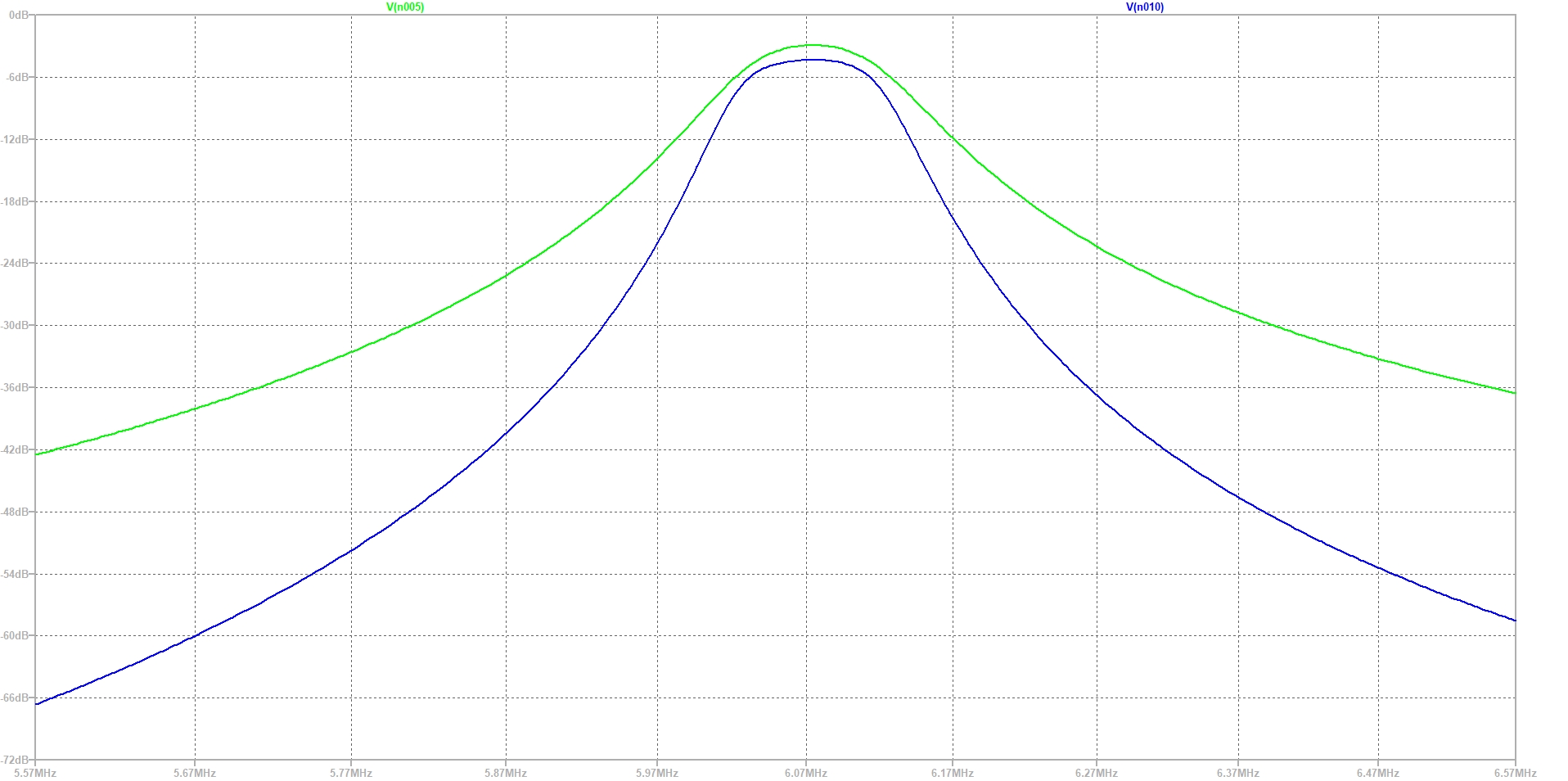
Wie zu erwarten, hat das Dreikreis-Filter eine höhere Durchgangsdämpfung als das Zweikreis-Filter, aber natürlich auch einen steileren Abfall außerhalb des Durchlassbereichs.
Als Nächstes ging ich daran, das Filter zu bauen. In irgendeiner Kiste fand ich noch ein paar Lufttrimmer, die sich für so eine Sache ganz gut eignen sollten.
Außerdem fand ich heraus, dass ein isolierter Volldraht, wie man ihn im Haus für die Elektroinstallation verwendet (mit 1.5qmm Querschnitt), ziemlich genau 50 Ohm Impedanz hat, wenn man ihn direkt auf eine leitende Oberfläche legt; in meinem Fall ein 160 mm langes Stück Cu-kaschiertes Leiterplattenmaterial. Mit so einer selbergebastelten 50-Ohm-Leitung kann man das HF-Signal prima vom Stecker zum ersten Filterelement leiten und vom letzten Filterelement zum Ausgangsstecker.
Weil ich sicher gehen wollte, bei meinen geplanten Experimenten später keine Aliasing-Probleme zu bekommen, habe ich gleich den Dreikreis-Filter aufgebaut. Der selbergebastelte Filter schaut so aus:

Für die Bewicklung der T50-6-Ringkerne verwendete ich 0.8mm-CuL-Draht.
Als Kapazitäten habe ich eingesetzt:
C_e: 56 pF || 6p8
C12: 6p8
C_m: 470 pF || 68 pF || Trimmer-C
C_t: 470 pF || Trimmer-C
Mit meinem VNWA3 habe ich die Übertragungsfunktion gemessen und die Trimmkondensatoren eingestellt: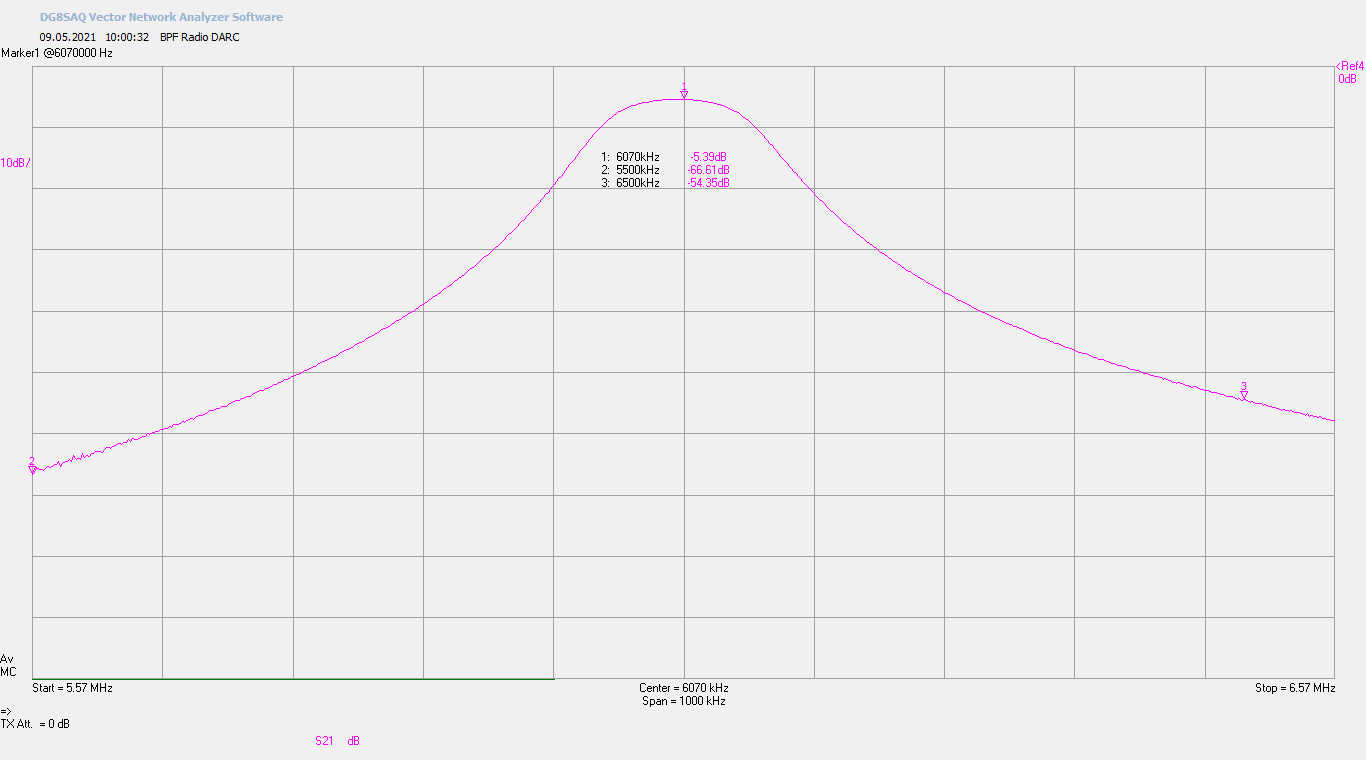
Als Durchgangsdämpfung habe ich in der Wirklichkeit einen etwas schlechteren Wert erreicht (-5.39 dB; durch Nachjustieren ein etwas besser Wert als die -5.76 dB, die auf dem Foto stehen) als es die Simulation vorausberechnet hat (-4.32 dB), aber das liegt wahrscheinlich an der etwas groben Abschätzung der Güte. Ich kann da wahrscheinlich ganz zufrieden sein?
Bei 5.57 MHz komme ich auf eine gemessene Dämpfung von -66.61 dB (Simulation: -66.63 dB) und bei 6500 KHz auf gemessene -55.34 dB (Simulation: -55.14 dB). Das ist eigentlich eine erstaunlich gute Übereinstimmung.
Die Weitab-Selektion im Frequenzbereich bis 30 MHz schaut aus wie folgt, wobei in diesem Diagramm jedes Kästchen 20 dB hoch ist und nicht 10 dB wie im vorigen Diagramm. Außerdem ist zu beachten, dass bei Dämpfungswerten größer als 90 dB das Rauschen schon eine erhebliche Rolle spielt; für das folgende Diagramm wurde also schon ordentlich gemittelt.
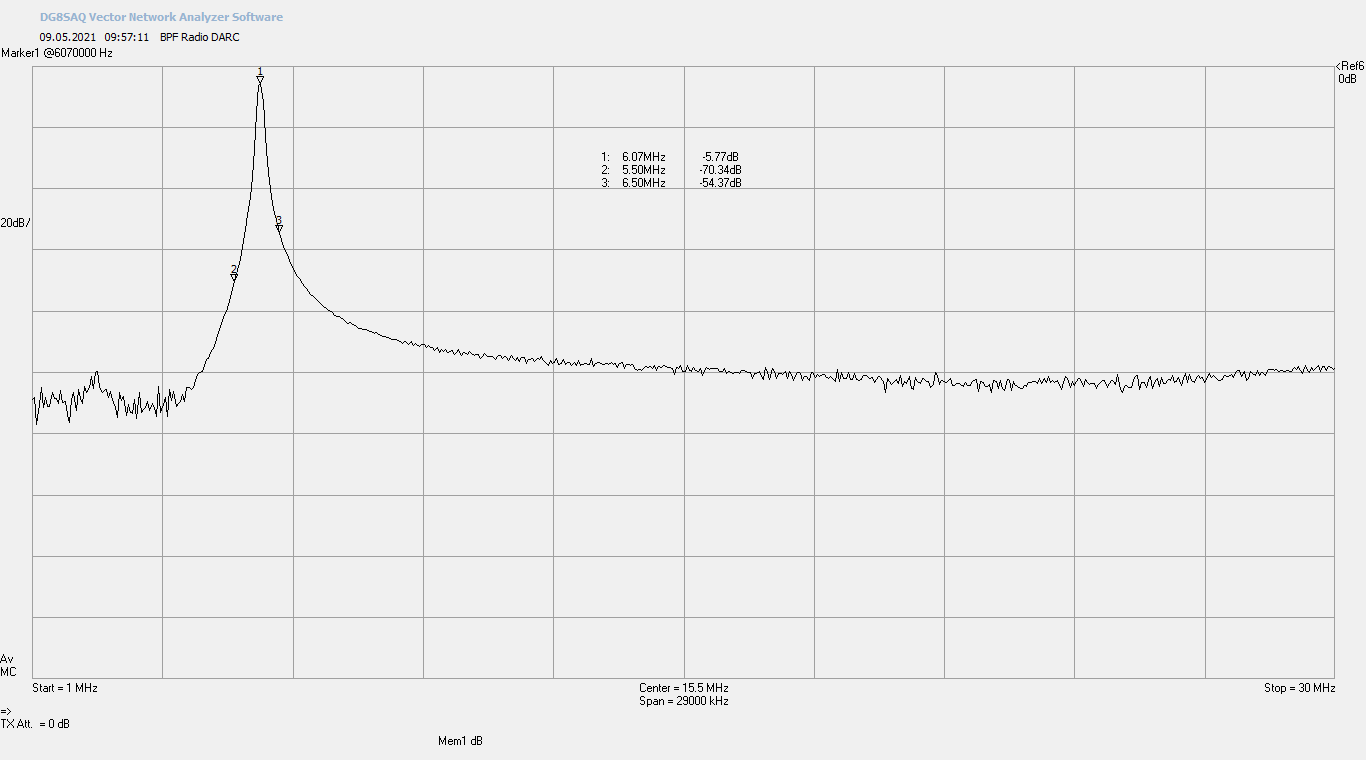
Für meine Zwecke sollte das Filter jedenfalls völlig ausreichen!
